| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- for문
- 정보보호
- 파이썬
- 딥러닝수학
- Python
- 딥러닝
- 딥러닝실행
- 프로젝트
- 스마트인재개발원
- 스마트인재개발원 후기
- 광주인공지능학원
- 문자태그
- Selenium
- 주식
- 딥러닝기초수학
- HTML
- java
- 멜론
- 보안
- 도서관관리
- 기본목록
- Visual Studio Code
- 머신러닝
- 웹툰
- 크롤링
- 보안용어
- 컴퓨터보안
- 크롬
- while문
- 웹 크롤링
- Today
- Total
자신의 일은 스스로하자
[딥러닝] #2 딥러닝 기초 수학 [광주인공지능학원] 본문

광주인공지능학원에서 진행된 수업입니다.
딥러닝을 배울 때 딥러닝 수학 원리를 공부하는 것도 중요합니다. 딥러닝 수학원리를 이해하기 위해서는 최소 고등학교 수준의 기본적인 수학 지식이 필요합니다. 어떤 원리로 입력 값의 패턴을 분석하고 학습하는지를 이해하려면 그 배경이 되는 수학을 살펴봐야 하고 사용되는 함수들을 알아야 합니다.

광주인공지능학원에서 배운 내용을 토대로 복습한 내용입니다.
1. 일차 함수, 기울기와 y절편
함수란 두 집합 사이의 관계를 설명하는 수학 개념입니다. 변수 x와 y가 있을 때, x가 변하면 이에 따라 y는 어떤 규칙으로 변하는지를 나타냅니다.
일차 함수는 y가 x에 관한 일차식으로 표현된 경우를 말합니다.

위 사진과 같은 함수 식으로 나타냅니다. x가 일차인 형태이며 x가 일차로 남으려면 a는 0이 아니어야 합니다.
일차 함수 식 y=ax+b에서 a는 기울기 b는 절편이라고 합니다. 기울기는 기울어진 정도를 의미합니다. x 값이 증가할 때 y 값이 어느 정도 증가하는지에 따라 그래프의 기울기 a 가 정해집니다. 절편은 그래프가 축과 만나는 지점을 말합니다. y축과 만나는 y절편이 b입니다. x가 주어지고 원하는 y값이 있을 때 적절한 a와 b를 찾는 것이 딥러닝을 설명하는 간단한 표현입니다.
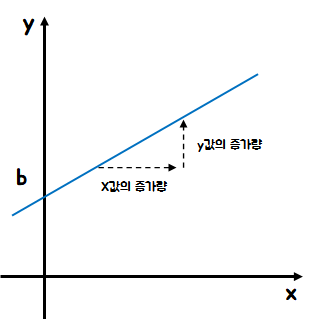
광주인공지능학원에서 배운 내용을 토대로 복습한 내용입니다.
2. 이차 함수와 최솟값
이차 함수한 y가 x에 관한 이차식으로 표현되는 경우를 말합니다.

이차 함수의 그래프는 포물선 모양입니다. a>0이면 아래로 볼록한 그래프가 됩니다.
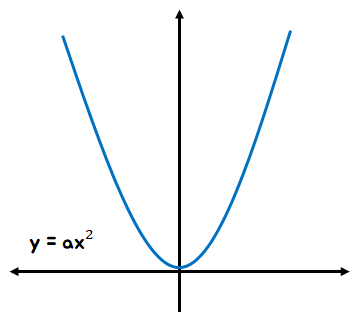
그래프를 x축 방향으로 p만큼, y축 방향으로 q만큼 평행 이동시키면 아래 사진과 같이 움직입니다. 점 p와 q를 꼭짓점으로 하는 포물선이 됩니다. 이때 포물선의 맨 아래에 위치한 지점이 최솟값이 되는데 이 최솟값을 찾아내는 과정이 딥러닝에서 매우 중요합니다.

최솟값은 최소 제곱 법공식으로 쉽게 알아낼 수 있습니다. 하지만 딥러닝을 실제 실행할 때는 대부분 최소 제곱 법을 사용할 수 없습니다. 최소 제곱 법을 계산하기 위해 필요한 조건들을 알 수 없기 때문입니다. 그래서 미분과 기울기를 이용해야 합니다.
지금까지 광주인공지능학원에서 배운 내용을 토대로 복습한 내용입니다. 미분과 기울기는 다음 포스팅에서 설명드리겠습니다.
광주인공지능학원에서 진행된 수업입니다.
http://www.smhrd.or.kr
스마트인재개발원
4차산업혁명시대를 선도하는 빅데이터, 인공지능, 사물인터넷 전문 '0원' 취업연계교육기관
www.smhrd.or.kr
'AI > 딥러닝' 카테고리의 다른 글
| [딥러닝] #6 딥러닝 기초수학 로그와 로그함수 [광주인공지능학원] (0) | 2021.08.30 |
|---|---|
| [딥러닝] #5 기초수학 시그모이드 함수/ 로그 / 로그 함수 [광주인공지능학원] (0) | 2021.08.30 |
| [딥러닝] #4 딥러닝 기초수학 / 편미분 / 지수 / 지수함수 [ 광주인공지능학원] (0) | 2021.08.23 |
| [딥러닝] #3 딥러닝 기초수학 / 미분 / 순간 변화율과 기울기 [광주인공지능학원] (0) | 2021.08.23 |
| [딥러닝] #1 딥러닝이란 / 딥러닝 실행을 위한 준비 사항 [광주인공지능학원] (0) | 2021.08.09 |




